Undergraduate course in Differential Equations
MATH 2552
Georgia Institute of Technology, Fall 2024
Contact: glivshyts6@math.gatech.edu
Location and time: the class lectures meet virtually Tuesdays/Thursdays 9:30-10:45am via Zoom
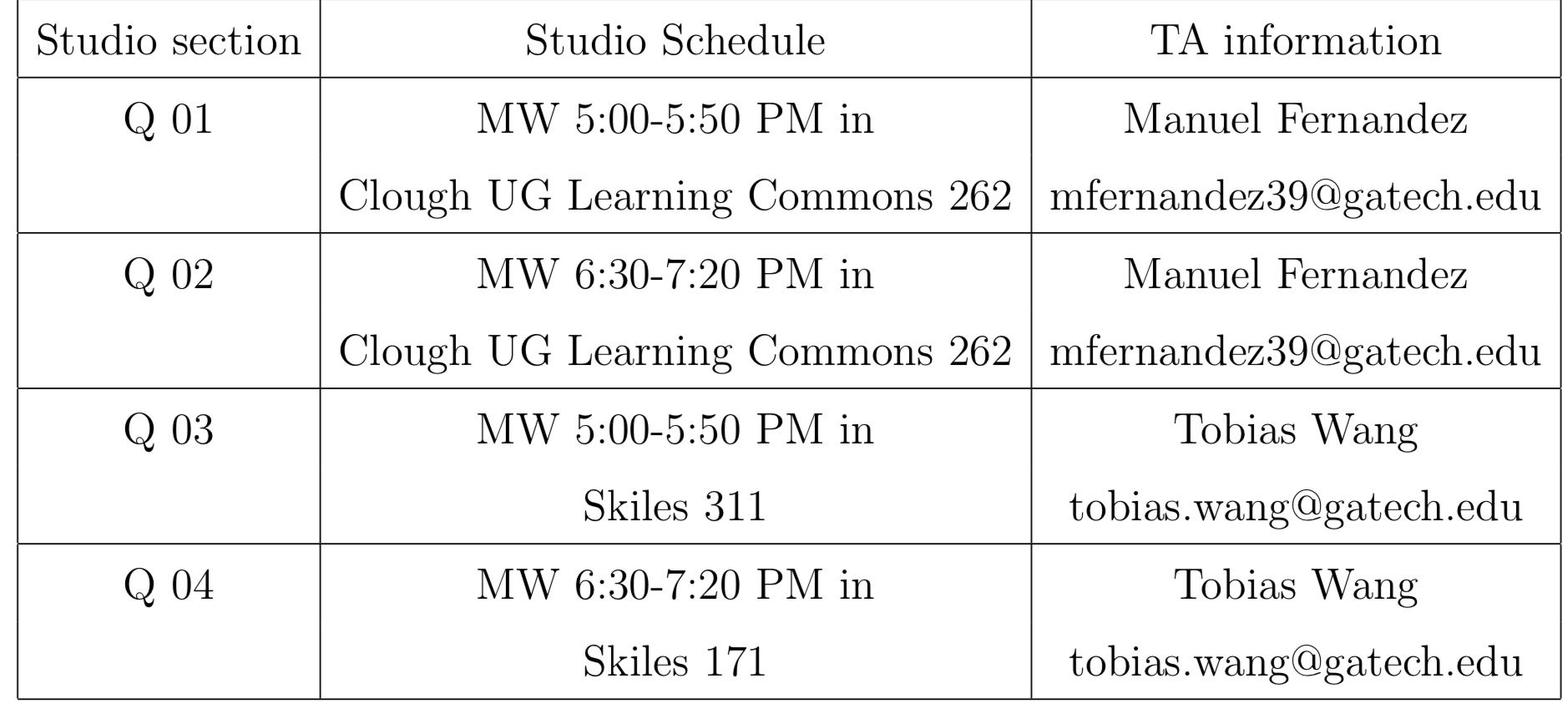
August 19 through December 3, 2024. For the studio times, consult the syllabus.
Office hours: Monday at 9-11am online via Zoom.
Description: In this course, we cover various analytic solution methods of elementary differential equations, applications of differential equations to real world problems with modeling, qualitative studies of solutions emphasizing stability/instability. See the syllabus for more details. All the course announcements will be made via Canvas. Please make sure to follow Canvas updates. In person attendance is expected for the studios, and virtual attendance and active participation is expected for the Zoom lectures; both shall be rewarded with extra credit.
Textbook: "Differential Equations (an introduction to modern methods and applications)", James R. Brannan and William E. Boyce,3rd edition. We will cover Chapters 1-8.
Homework: assigned via WebWorks weekly
Grading:
For more details about the grading policies and extra credit opportunities, consult the syllabus. You may view your up to date grades via Cavas or Gaderscope.
Class whiteboard:
Lectures 1-2:TBD.